Non-Ideal Gases

Non-Ideal Gases

An ideal gas is a theoretical idea – a gas in which there are no attractive forces between the molecules, and in which the molecules take up no space. Both of these assumptions are incorrect.

if there were no attractive forces between molecules, no substances would ever condense from the gas state to become liquids and solids. In fact, every substance does condense when it is cooled and compressed enough. Therefore there must be attractive forces between molecules.
if molecules took up no space, then we could compress substances until they had no volume at all. In fact, solids and liquids are almost incompressible, since their molecules are basically touching each other. Since solids and liquids take up space, the molecules of which they are made must take up space also.

However:

when the pressure is fairly low (around atmospheric pressure or less) the molecules are not very close to each other. The intermolecular attractions and molecular size are not very important under these conditions.
when the temperature is fairly high (perhaps 100 ^oC or more above the substance's boiling boint) the attractive forces are not very important compared to the rapid motion of the molecules

Under these conditions, a gas will behave nearly ideally. This is true for things we readily identify as gases at room temperature and pressure conditions, like hydrogen, nitrogen and oxygen. These real gases are said to behave ideally – that is, they obey the ideal gas law.

In this experiment you will measure the Pressure – Volume behavior of a gas that is not ideal. The gas used will be butane. Most of us are familiar with a disposable butane lighter. Under a moderate amount of pressure, the butane (iso-butane actually) is in the liquid state at room temperature. We know that the pressure can’t be too high, because the lighter is made of fairly thin plastic that would not stand a high pressure. When the pressure is released, the butane liquid vaporizes, and becomes a gas, since the boiling point of iso-butane is –11.7 ^oC, approximately 35 degrees below room temperature. These characteristics:

low pressure required to condense the gas

boiling point close to room temperature

suggest that iso-butane probably deviates a lot from ideal gas behavior.

To demonstrate non-ideal behavior, iso-butane will be compressed in a disposable syringe while measuring the pressure exerted on the gas. A similar procedure will be carried out with air, which should have nearly ideal behavior. The ideal gas equation is often stated as pV = nRT. Dividing by V we could rewrite this as 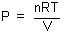. 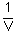Since we are going to work with a constant quantity of gas (n) at a single temperature (T), and R is also a constant, this means that a graph of P as a function of for an ideal gas should be a straight line passing through the origin.

Materials:

butane refill container
35 mL disposable syringe
Vernier pressure gauge
CBL system and TI calculator to collect data
short length of 1/8" vinyl tubing
masking tape, or bag and syringe assembly for gas storage (see teacher notes)

Procedure:

Caution: butane is highly flammable. Make certain that there are no open sources of flame, or spark in the lab. Dispose of the butane by venting it to the outdoors, or into a fume hood.

1. Fill the syringe to its maximum measured capacity with air.

2. Set up the TI calculator and CBL system to measure pressure. Plug the pressure gauge into channel 1. Make sure the connector between the CBL and TI calculator is firmly in place. Run the non-ideal gas program.

Select SET UP PROBES

Select INITIALIZE P

Set up the probe to measure P in channel 1.

Select UNITS-CALIB and choose the proper pressure unit

You need not set up the temperature, or do a calibration.

When the probe is set up go back to the MAIN MENU

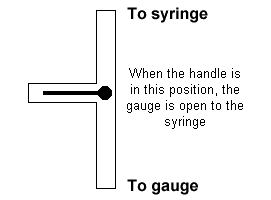
3. Attach the syringe to the Vernier pressure gauge. Open its three way valve to the atmosphere, and adjust the volume to the highest volume marked on the syringe. Then close the valve so that the gas pressure can be measured.

CAUTION: In making the following pressure measurements, make sure you hold the syringe at the top so that the temperature of the gas is not affected by heat from your hand.

Select GET AIR P
Adjust the plunger to the maximum volume calibration. Press the [TRIGGER] button on the CBL when ready to measure the pressure
Enter the volume recorded from the syringe (or, if you know that the point is in error, enter a 0 which will let you redo the point.

4. You need to collect data for at least 5 points, going to the highest pressure you can reach. It is very important to reach the maximum pressure possible by hand, without going over the limit of about 600 kPa. This is about the amount of pressure a strong person can exert with one hand. If using a 35 mL syringe, you should be able to go to a minimum volume of 10 mL or less.

5. Move the plunger to a lower volume and repeat the pressure measurement. If you use a 35 mL syringe, then you should be able to make pressure readings at 35, 30, 25, 20, 15, 10 mL. It may be possible to get the volume close to 5 mL; however, it is very hard to get stable readings at this level. If two people work together -- one to compress the gas and hold the syringe while the other presses the trigger button you will be more successful. It is most important to get a stable pressure reading, so if you are not strong enough to compress the gas below 10 mL and hold it steady, get it to as small a stable volume as possible.

Caution: Do not go below 5 mL, as the pressure will become so high it may damage the pressure gauge.

6. Plot the GRAPH of the data. Since air is very nearly an ideal gas, even at the maximum pressure you can reach in this experiment, a graph of p (on the Y or vertical axis) and 1/V (on the X or horizontal axis) should be an almost perfectly straight line. If there is a lot of deviation from a straight line plot for the air, you should repeat the measurements for air.

7. Now, fill the syringe with butane. Push the plunger of the syringe to 0, and attach it to the source of butane. Pull back the plunger of the syringe to fill it with butane. Remove the syringe assembly from the butane source, and attach it quickly to the pressure gauge.

Select GET BUTANE P from the menu
Adjust the plunger to each of the volumes you measured in step 3, and press the [TRIGGER] button on the CBL when the pressure is stable.

8. Select GRAPH to see both the air pressure, and butane pressure graphs together. You should notice both some similarities, and differences between the two graphs. NOTE: the graph displayed is a plot of p vs 1/V, which should be a straight line for an ideal gas.

9. Select VIEW DATA and copy down the measured data points into a table.

L1 is the volume
L2 is the air pressure data
L3 is the butane pressure data

Analysis:

1. How different are the plots of p vs 1/V for air and iso-butane at

low pressures?
high pressures?

2. Is the pressure of the iso-butane greater than, or less than the pressure of the air when compressed to the same volume? Explain the reason for this behavior.

3. According to your data, how much error will you have if you assume ideal gas behavior for iso-butane at pressures of 1 atm (100 kPa) or less? How much error would you have at 2 atm (200 kPa)? How about at 5 atm (500 kPa)? HINT: to answer this question, consider the answer for air at these pressures to be the correct value, and estimate the pressure of the butane from the plot of p vs 1/V at the same volume.

4. According to your answer for question 3, could you use the ideal gas equation safely for iso-butane at near room temperature and pressure conditions?