To add or subtract numbers using the rules for significant digits, you need to keep this idea in mind: you can't add or subtract from something you do not know.

Suppose that the population of a small city is about 3.0 x 10⁴ people (that's 30,000 but we've written it in this way to emphasize that we are not sure about the population at the second digit in the number.  This is just a population estimate and we have two significant figures).  During one month, 35 babies are born, and 13 people move away.  Does this mean that the population is now 30022 people?  Not really.  Do we know that the population of this city increased by 22 people this month?  Yes, definitely.

Here's why (color coding is used in the following diagram to illustrate the significant digits).  When you add a number to a number you do not know (the red digits in the original population), you have an answer that is just as unknown.  The last three digits are still not signficant.  The answer can still only be reported to the first two significant digits as 3.0 x 104 people.
However, when we subtract the migration from the births we get the population change, and that result will retain two digits of accuracy.  Both 35 and 13 have two digits of accuracy.  We are subtracting from a value we know.

The best method for keeping track of significant digits in addition and subtraction questions is to write the problem down as if you were going to do it by hand (though you may well use a calculator to do the actual math).  Make sure the numbers are aligned at the decimal point.  Add and subtract to get the full answer, then round it off at the farthest left significant digit in the answer.  Here are a few more examples:

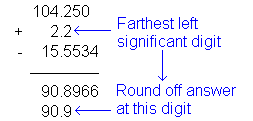«««« Report this answer as 90.9   Report this answer as -0.105 »»»»

Try a number of these problems for practice.

Adding and subtracting numbers that are written in scientific notation is a bit more complex.

Click to see how to add and subtract numbers written in scientific notation.