If you are going to understand significant digits, you have to be sure you are recording your measurements properly. Sounds simple, right? And it is, yet it also has a few "gotcha's" to be careful about.
For example, suppose that you were told to measure the length of the green line, using a normal centimetre ruler.
Most of us wouldn't have much trouble at all indicating that the line is longer than 9 cm, but not quite 10. Therefore we would be absolutely positive in reporting that the line is between 9 and 10 cm long. We can pretty easily tell that the line is more than 9.5 and less than 9.7 cm long, so we could be sure about reporting the line to be 9.6 cm. In fact, since it looks like the line is exactly 9.6 cm long, you might be tempted to record its length as 9.6 cm.
If you did so, you would be wrong. If the line was 9.58 cm long, or 9.62 cm long,
you would be able to see that it didn't line up precisely with the 9.6 cm mark. You
are really measuring more accurately than to the nearest tenth of a centimetre. You
can with some confidence indicate that the line is 9.60 cm long. But you are not
really positive. Perhaps it is 9.59 cm long, or 9.61 cm long. It would be hard
to tell the difference with the naked eye more precisely than that. The uncertainty
limit is about 0.02 cm when using an ordinary ruler. Therefore you should report
your answer to two hundredths of a centimetre, which in this case is 9.60 cm.
| Could we perhaps improve the measurement by using a high powered magnifying glass to
get better results, allowing us to measure to the nearest 1/1000 of a centimetre? Not really. If you did this then you would probably find that the green line doesn't have a perfect edge, the lines on the ruler aren't really lines, but have a thickness, and the manufacturer can't make the lines perfectly even in any case. We can't legitimately report that the line is 9.600 cm long, because our measurement ability, and the instrument itself just aren't that good. |
 |
Thus the proper way to record the length of the line is 9.60 cm, not 9.6 or 9.600. Mathematically 9.6, 9.600 and 9.60 are the same, but experimentally they are not. The number 9.60 indicates that the measurement was made more precisely than the number 9.6 does. It shows that we know the length approximately to the nearest hundredth of a centimetre, but we don't really know the length to the nearest thousandth of a centimetre.
|
What we are doing here is using the concept of significant digits. Think about the original ruler. We record all the numbers of which we are certain (the 9.6) and the first digit we are not sure of (the 0.00). The number must be recorded as 9.60. Now just count the digits in this number. There are three, so 9.60 has 3 significant digits.
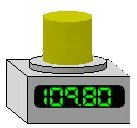
| If we assume that the following number was measured experimentally, and recorded properly, then how many significant digits does it contain? |
Record your results with all the digits that you can measure, to the limit of the uncertainty of the equipment. Make sure to include zeroes when they are actually being measured. General RulesOn a digital instrument, read and record all the numbers, including zeros after the decimal point, exactly as displayed.On a scaled instrument, estimate one more figure than you can actually read from the scale. |
Usually the manufacturer of the equipment indicates how accurately or precisely it can measure. This
tells you how many digits you should record when using this device. For example,
suppose that the manufacturer of a graduated cylinder indicates that it is accurate
to 
0.5
mL. If you use such a graduated cylinder to measure the volume of a substance,
then you should only report it to the nearest half millilitre – 95.0, 95.5, 96.0,
etc.
Here are some examples of measurements that can be made with equipment found in a
typical high school science classroom.
| Device | Typical uncertainty | Typical Measurement |
| 50 mL graduated cylinder | 0.2 mL |
48.0 mL |
| 200 g digital balance | 0.01 g |
140.00 g |
| -10 to 110 oC thermometer | 0.2 oC |
25.0 oC |
| 50 ml buret | 0.02 mL |
28.00 mL |
These are typical uncertainties. The actual uncertainty in a particular instrument may be greater or smaller. As well, the uncertainty depends on the skill of the observer. Making accurate, precise, observations is a skill that takes practice. Some instruments are very easy to use – a digital balance for example – and you will probably be able to make measurements at the actual uncertainty of the instrument on the first try. Reading the volume on a graduated cylinder takes a lot more practice.
|
|
 |
Try the quiz to see if you have the idea.
